Не все так просто: средняя скорость и среднее арифметическое — в чем разница?

Неплохо? Давайте проверим, насколько вы усвоили программу и помните ли вы её вообще?

Дано: гоночный болид, который преодолевает круг со средней скоростью 100 километров в час. Вопрос следующий: какую скорость должен развить пилот болида, чтобы общая средняя скорость равнялась 200 километрам в час?

Я думаю, многие из вас обрадовались, что даже калькулятор не понадобится для сложных вычислений. Скорость нужно увеличить в три раза и проехать круг со скоростью 300 километров в час. Потому что если к 100 прибавить 300 и разделить на 2, то получатся те самые искомые 200 километров в час.

А вот и нет! Не путайте понятия. Вы сейчас, конечно, нашли нечто среднее, но не среднюю скорость, а среднее арифметическое, что не является одним и тем же. Не понимаете?

Попробуем разобраться. Чтобы соответствовать условию задачи и поддерживать среднюю скорость в 200 километров в час, пилоту болида нужно ехать со скоростью 300 километров в час, только не на протяжении одного круга, а в течение одного часа.

Что, и так непонятно? Хорошо. Договоримся, что длина круга равна 100 километрам. Гонщик преодолевает это расстояние за один час. Если же его скорость будет равна 300 километрам в час, тогда он за то же самое время должен будет проехать уже в три раза больше, чем в начале, а значит — три круга. Тогда он преодолеет 400 километров со скоростью 200 километров в час. Но только вопрос в задаче другой — нам необходима средняя скорость 200 километров в час, достигнутая за один круг.

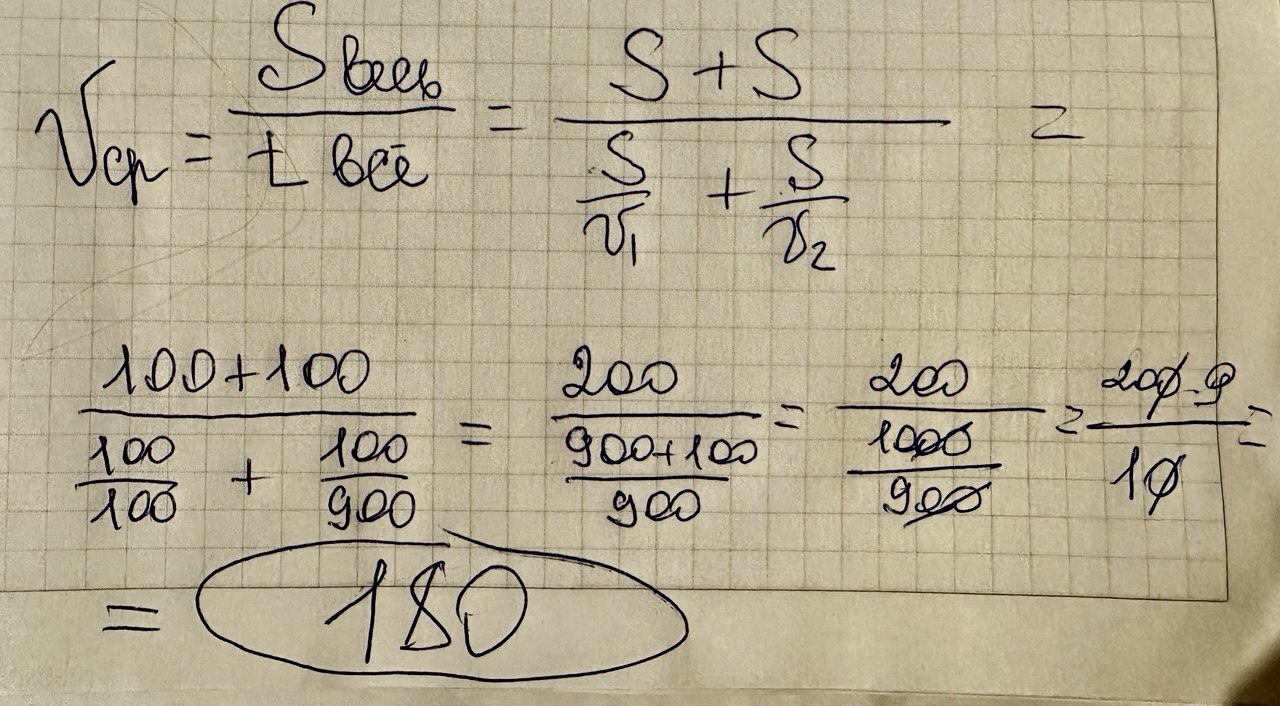
Попробуем добиться этого, увеличив скорость болида на втором круге в три раза. Тогда она будет достигать 900 километров в час (все логичные возгласы о том, что такой скорости добиться невозможно, сейчас не принимаются).

Но и в этом случае скорость будет меньше, а именно 180 километров в час (как мы получили эту цифру — на рисунке ниже).

Ещё одна попытка: увеличиваем скорость на втором круге до запредельных показаний. Да можете делать всё, что угодно, всё равно ничего не выйдет! Заменим цифры, чтобы считать было удобнее: круг теперь будет протяженностью 200 километров и тогда средняя скорость 200 километров в час должна быть достигнута при преодолении одного круга за один час. Но за час гонщик проедет лишь 100 километров, а это всего лишь половина пути.

И сколько бы вы не меняли длину круга, запрашиваемый ответ у вас не получится. Потому что средняя скорость, о которой идет речь в задаче, и среднее арифметическое, которое мы так легко находим — это абсолютно разные величины.

Напомним, ранее мы предлагали решить задание, с которым справляются даже шестилетние дети.

Надежда Сергеева

Фото: Freepik